今回の学習ターゲット
【DS7】積分と面積の関係を理解し、確率密度関数を定積分することで確率が得られることを説明できる
こんにちは。塾長の鬼MARUです。
今日は積分の概念を、実際のデータサイエンスの応用例を交えながら説明しますね。
特に以下のワードについて学びます:
- 定積分
- 不定積分
- 面積
- 確率密度関数
- 原始関数
- 被積分関数
積分とは?
積分は、関数のグラフと軸の間に囲まれた面積を求める数学的な操作です。
具体的には、ある関数 \( f(x) \) があったときに、積分記号 \( \int \) を使って次のように表します:
不定積分:
\[
\int f(x) \, dx = F(x) + C
\]
ここで、\( F(x) \) は原始関数と呼ばれ、微分すると元の関数 \( f(x) \) に戻ります。\( C \) は積分定数と呼ばれます。
定積分:
\[
\int_a^b f(x) \, dx = F(b) – F(a)
\]
ここで、定積分は \( x = a \) から \( x = b \) までの間に囲まれた面積を求めます。
定積分と面積の関係
関数が正(つまり \( f(x) \geq 0 \))のとき、定積分で計算される値はグラフの面積になります。例えば:
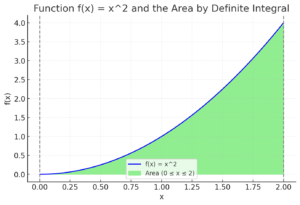
関数 \( f(x) = x^2 \) のグラフについて、\( x = 0 \) から \( x = 2 \) までの面積を計算します。
\[
\int_0^2 x^2 \, dx = \left[ \frac{x^3}{3} \right]_0^2 = \frac{2^3}{3} – \frac{0^3}{3} = \frac{8}{3}
\]
確率密度関数と積分
データサイエンスでは、確率密度関数(Probability Density Function, PDF)を使って確率を計算することが多いです。
確率密度関数には次の性質があります:
- \( f(x) \geq 0 \)(関数の値は非負)
- \( \int_{-\infty}^\infty f(x) \, dx = 1 \)(全体の面積が1)
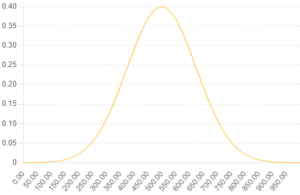
例えば、正規分布(ガウス分布)という有名な分布の確率密度関数は次の形をしています:
\[
f(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}}
\]
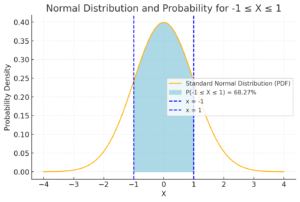
この関数を使って、\( x \) が \(-1\) から \( 1 \) の範囲にある確率を計算するには:
\[
P(-1 \leq X \leq 1) = \int_{-1}^1 f(x) \, dx
\]
数値的に計算すると約 68.27% の確率となります。これが、「-1 から 1 の範囲内にデータが存在する確率」です。
被積分関数と原始関数
積分記号の中にある関数 \( f(x) \) を被積分関数と呼びます。不定積分を行うと、この関数に対応する原始関数 \( F(x) \) を見つけることになります。
例えば、被積分関数 \( f(x) = x^2 \) の原始関数は:
\[
F(x) = \frac{x^3}{3}
\]
となります。この原始関数を使って定積分を計算できます。
まとめ
今日は、積分の基本的な考え方から、面積との関係、さらに確率密度関数の応用までを学びました。
特にデータサイエンスでは、確率密度関数を使ってデータの範囲を理解したり、確率を計算することが非常に重要です。